Международная школа-семинар

«Современные материалы с искусственной структурой»

Московский государственный университет имени М.В. Ломоносова

Механико-математический факультет, кафедра теории пластичности

22 – 24 июля 2019

ТЕЗИСЫ ДОКЛАДОВ

Применение асимптотического метода осреднения к дисперсным композитам

Артамонова Н.Б.

Московский государственный университет имени М.В. Ломоносова, Москва

Работа посвящена определению эффективных упругих модулей дисперсного композита Al2024/B₄C с помощью асимптотического метода осреднения, хорошо известного в механике композитов [1,2]. Вычислительный метод основан на асимптотическом осреднении уравнения равновесия неоднородного упругого материала и решении задач в представительной области.

Исследуемые композиты, состоящие из сплава Al2024, армированного частицами B₄C, были изготовлены способом плазменно-искрового спекания. В качестве 2D моделей для расчета эффективных свойств использовались оцифрованные фотографии плоских срезов композитов Al2024/B₄C с различным содержанием B₄C, полученных с помощью сканирующего растрового электронного микроскопа (РЭМ). 

Для проведения расчетов в композите было выделено 2 материала: 1) матрица, состоящая из Al и мелких (размером <1 мкм) включений Al₂Cu и B₄C; 2) более крупные включения карбида бора B₄C (размером от 7 до 30 мкм, средний размер – 10-20 мкм). Осреднение проводилось в 2 этапа. На 1-м этапе определялись эффективные упругие модули 3-х-компонентной матрицы, на 2-м этапе вычислялись эффективные свойства двухкомпонентного материала, состоящего из матрицы (с уже известными свойствами) и крупных включений B₄C.

Задача состояла в том, чтобы на основе двумерной оцифрованной структуры неоднородностей материала оценить эффективные упругие свойства реального трехмерного дисперсного композита. Для этого использовались два подхода: решались двумерные задачи при плоско-деформированном и плоско-напряженном состояниях в конечно-элементной программе, затем результаты сравнивались. Оказалось, что значения модуля Юнга, вычисленные для плоских деформаций и плоских напряжений, отличаются не более чем на 1%  (при одинаковых значениях содержания B₄C), что позволяет сделать вывод о достоверности результатов расчета и подтверждает возможность использования двумерных изображений для вычисления эффективных упругих модулей реального композита.

По результатам расчетов была получена зависимость модуля упругости дисперсного композита Al2024/B₄C от содержания в нем армирующих частиц карбида бора. Для концентраций включений до 20% данная зависимость фактически является линейной.

Работа выполнена при поддержке гранта РФФИ № 19-51-53006. 

Литература

1. Бахвалов Н. С., Панасенко Г. П. Осреднение процессов в периодических средах. М.: Наука, 1984. 352 с.

2. Победря Б. Е. Механика композиционных материалов. М.: Изд-во МГУ, 1984. 336 с.

Экспериментальная верификация вычисления эффективных упругих модулей и параметра Био природных композитов

Артамонова Н.Б., Шешенин С.В., Фролова Ю.В., Новиков П.В., Бессонова О.Ю.

Московский государственный университет имени М.В. Ломоносова, Москва

В работе предложено практическое приложение асимптотического метода осреднения [1] для определения эффективных упругих модулей [2] и параметра Био [3] природных композитов на примере карбонатных пород (доломитов и известняков) и вулканогенно-осадочных пород (гиалокластитов). Предлагаемая вычислительная методика позволяет рассчитывать тензорный параметр Био для случая общей анизотропии породы, скелет которой имеет неоднородный минеральный состав [3]. Метод основан на асимптотическом осреднении уравнения равновесия неоднородного упругого пористого материала и решении задач в представительной области [3].

Цель работы состояла в том, чтобы оценить эффективные свойства исследуемых пород предлагаемым вычислительным методом и сравнить полученные данные с результатами опытов. Для этого было проведено комплексное экспериментальное исследование карбонатов и гиалокластитов. Микроскопическая структура пород изучалась в шлифах под микроскопом, минеральный состав определялся методом рентгеновской дифрактометрии. Упругие модули пород определялись по методике ультразвукового просвечивания образцов.

Эффективные упругие модули пород оценивались по методу осреднения на основе двумерных моделей, построенных в результате ручной оцифровки фотографий шлифов –неоднородностей скелета пород и структуры порового пространства. Так как эффективные свойства оценивались по результатам решения плоской задачи, то для проверки достоверности результатов расчета использовались два подхода: двумерные задачи решались при плоско-деформированном и плоско-напряженном состояниях, а затем результаты сравнивались. Значения модуля Юнга карбонатов, вычисленные для плоских деформаций и плоских напряжений, получились близкими (при одинаковых значениях пористости). Также было проведено сравнение результатов вычислений с данными экспериментов, которое показало хорошее совпадение. Все это свидетельствует о достоверности результатов расчета и подтверждает возможность использования метода осреднения для оценки эффективных упругих свойств скальных грунтов по двумерным изображениям шлифов.

Вычислительная методика позволяет изучать влияние пористости, формы и ориентации пор на значения модуля упругости и параметра Био. По результатам расчетов и экспериментов для доломитов и известняков были получены зависимости модуля упругости и коэффициента Био от пористости, которые могут иметь практическое значение. С увеличением пористости модуль упругости уменьшается, а параметр Био увеличивается. Влияние формы пор на упругие модули и коэффициент Био исследовалось на примере образцов гиалокластитов двух типов – с круглыми и угловатыми порами. При одной и той же пористости у образцов с круглыми порами модуль Юнга выше, а коэффициент Био ниже, чем у образцов с угловатыми порами. Влияние ориентации пор изучалось на примере анизотропных образцов доломита, характеризующихся вытянутыми ориентированными порами. Расчеты показали, что вдоль вытянутости пор параметр Био ниже, чем поперек (для модуля упругости зависимость обратная).

Литература

1. Бахвалов Н. С., Панасенко Г. П. Осреднение процессов в периодических средах. М.: Наука, 1984. 352 с.

2. Победря Б. Е. Механика композиционных материалов. М.: Изд-во МГУ, 1984. 336 с.

3. Artamonova N. B., Mukatova A. Zh., Sheshenin S. V. Asymptotic analysis of the equilibrium equation of a fluid-saturated porous medium by the homogenization method // Mechanics of Solids. 2017. Vol. 52, No. 2. P. 212—223.

Влияние масштаба на изгибную жесткость пластины с искусственной структурой

Волков Л.С.

Московский государственный университет имени М.В. Ломоносова, Москва

            Доклад посвящен описанию поведения материалов с искусственной структурой. Смоделированы плоские прямоугольные ячейки периодичности с полукольцевым и полуэллиптическим включениями. Из ячеек периодичности каждого вида собирались ансамбли размера p ячеек в высоту и 4 ячейки в ширину (p — параметр). Для полукольцевых ячеек 1 ≤ p ≤ 5, для полуэллиптических ячеек 1 ≤ p ≤ 10. Все ансамбли подвергались растяжению вдоль оси OX и рассматривалось изменение выражения, равного отношению среднего момента относительно закрепленной стороны к величине растягивающей силы, помноженной на толщину ячейки, в зависимости от роста p. Полученные результаты удовлетворяют теории, разработанной С.В. Шешениным.

Численное исследование эффективных свойств композита B₄C/Al на основе модельной структуры

Волков М.А., Киселев Ф.Б.

Московский государственный университет имени М.В. Ломоносова, Москва

            Работа посвящена сравнению эффективных упругих модулей, полученных для модели композита с матрицей из алюминия и включениями карбида бора. Модули определялись из численных экспериментов в 2D и 3D постановках. Включения в модели материала имели форму цилиндров и эллипсоидов с хаотической ориентацией. Геометрические характеристики модельных включений имели то же вероятностное распределение, что и в реальном материале. Из решения в трехмерной постановке серии задач для ортотропного материала показано, что при объемной концентрации включений до 20% материал проявляет свойства изотропии по каждому из трех ортогональных направлений. Полученный вывод соответствует и рассчитанным аналитически эффективным свойствам композита с включениями сферической формы.

            Кроме того, проведено сравнение значений для эффективных модуля Юнга и коэффициента Пуассона, полученных из численного решения задач в плоской и трехмерной постановках в предположении изотропии свойств биметаллического сплава. Для плоской задачи модельная область строилась, как плоское сечение кубической модели материала.  При этом выбирались такие плоские сечения, процентная концентрация включений в которых совпадала с ее значением для трехмерной области. Рассчитанные численно эффективные модули сравнивались с имеющимися экспериментальными значениями для процентных концентраций включений, равных, соответственно, 5%, 10% и 15 %. Плоская задача решалась численно в двух постановках: для плоско-деформированного и плосконапряженного состояний материала. Проведенные вычисления позволяют сделать следующие выводы. Разность между экспериментальными и вычисленными в трехмерной и плоских постановках значениями эффективного модуля Юнга рассматриваемого композита для всех трех процентных концентраций включения не превышают 5 %. Эта разность растет с ростом процентной концентрации включений. Для эффективного коэффициента Пуассона при малых процентных концентрациях включений лучшее приближение к экспериментальным и полученным из решения задач в трехмерной постановке значениям дает плоская задача для плосконапряженного состояния. С ростом процентной концентрации включений лучшее приближение для эффективного коэффициента Пуассона обеспечивает решение плоской задачи для плоско-деформированного состояния. При этом, при 15% содержании включений в материале разница между экспериментальным значением коэффициента Пуассона и значением, рассчитанным для плосконапряженного состояния, составляет 14%. Проведенное исследование может быть полезно при моделировании поведения сплава B₄C/Al в трехмерных задачах в случае, когда имеется фотография плоского среза реального материала и эффективные свойства материала необходимо определить по ней из численного эксперимента. В дальнейшем, проведенное исследование будет использовано при численном моделировании динамического поведения сплава B₄C/Al.

            Работа выполнена при поддержке гранта РФФИ № 19-51-53006. 

Влияние связанности механического и температурного полей на решение задачи термоупругости

Киселев Ф.Б.¹, Сергеев Ф.В.²

¹Московский государственный университет имени М.В. Ломоносова, Москва

²НИУ Московский государственный строительный университет, Москва

Доклад посвящен определению изменяющихся совместно полей температур и деформаций во влажном грунте, претерпевающем фазовые переходы. Изменение полей температур и деформаций грунта вызваны разогревом грунта от находящегося на его поверхности сооружения, сезонным колебанием температуры и давлением сооружения на грунт. Предполагается, что часть грунта находится в многолетнемерзлом состоянии, и сам грунт имеет слоистую структуру. Задача ставится в так называемой обобщенной формулировке Стефана, когда условие на скачок теплового потока на поверхности раздела фаз формулируется в виде массового источника или стока тепла в искусственно введенном слое, содержащем поверхность раздела фаз. Решается задача численно в квазистатическом приближении, методом сквозного счета, в связанной постановке. Эффект связанности появляется из-за взаимного влияния пространственной деформации грунта и изменения в нем поля температуры. Оценка его влияния на развитие во времени осадки сооружения является целью данного доклада. Задача обладает свойством квазилинейности из-за зависимости коэффициентов уравнений и граничного условия третьего рода для температуры от самой температуры. Поэтому оценка эффекта связанности уравнений на решение проводится на примере конкретной задачи, имеющей прикладное значение. В качестве сооружения выступает газофакельная установка (ГФУ) с защитным амбаром, представляющим собой конструкцию из плит жаропрочного бетона, заполненную слоями уплотненного песка, теплоизоляции (вспученного вермикулита) и противофильтрационного экрана. Подобные ГФУ являются элементами газопроводов и обслуживают куст газодобывающих скважин. Разогрев поверхности амбара в режиме активной работы установки достигает 1000 С⁰, что способно вызвать протаивание толщи многолетнемерзлых грунтов, расположенных под установкой, и привести к недопустимым осадкам в зоне расположения установки. Существенное влияние на растепление многолетнемерзлых грунтов оказывает и сезонное изменение солнечной радиации и температуры окружающего воздуха. Уравнение теплопроводности, записанное в вариационной форме для пробной функции , с учетом соответствующего граничного условия для нормальной составляющей  потока вектора солнечной радиации через границу, имеет вид:

Учет солнечной энергии в этом уравнении является сложной задачей, поскольку значение параметра  зависит от трудно определяемых факторов, таких, как растительный и снежный покровов, доля длинноволнового излучения, отраженного атмосферой в сторону поверхности Земли, которые в конкретной географической местности, как правило, не известны.

Определение параметра  будем проводить с помощью итерационного процесса, считая, что для заданной географической точки нам, кроме климатических данных, известно распределение температуры в грунте по глубине для заданного момента времени. Координатно-временная аппроксимация вариационных уравнений задачи термоупругости осуществлена с помощью МКЭ и неявной схемы Эйлера.

Решение рассмотренной прикладной задачи позволяет осуществить оптимальное проектирование защитного амбара под ГФУ с точки зрения выбора толщин теплоизоляционных слоев, позволяющих, с одной стороны, аккумулировать в подстилающих многолетнемерзлых породах отрицательные температуры холодных годовых сезонов, а с другой стороны, осуществлять их эффективную теплоизоляцию от работающих газофакельных установок.

Численное моделирование материалов с искусственной структурой

Семенов Д.М.

Московский государственный университет имени М.В. Ломоносова, Москва

В докладе продемонстрированы результаты, полученные в ходе применения различных подходов к численному моделированию материалов с искусственной трёхмерной структурой. Исследуется зависимость проявления моментных свойств от масштабного фактора. Посредством проведения серии численных расчётов получены эффективные модули осреднённого материала, что используется для сравнения поведения конструкции, смоделированной из реального материала с конструкцией из осреднённого материала.

Результаты численного эксперимента показывают, что коэффициент , связывающий нормальные напряжения с поворотом, может существенно зависеть от соотношения  характерного размера ячейки периодичности к характерному размеру всей конструкции. Показано, что уже при переходе от единичной ячейки к конструкции c  может наблюдаться значительное падение значения коэффициента , а при  наблюдается линейная зависимость между  и .

Литература

1. Кристенсен Р. Введение в механику композитов. М.: Мир, 1982. 336 с.

2. Minghui Fu, Fengming Liu, Lingling Hu. A novel category of 3D chiral material with negative Poisson's ratio // Composites Science and Technology. 2018. Vol. 160. P. 111—118.

3. Ming-Hui Fu, Bin-Bin Zheng, Wei-Hua Li. A novel chiral three-dimensional material with negative Poisson’s ratio and the equivalent elastic parameters // Composite Structures. 2017. Vol. 176. P. 442–448.

Жесткостные свойства резинокордного слоя

Шешенин С.В., Клементьев П.Д.

Московский государственный университет имени М.В. Ломоносова, Москва

Резинокордный слой является композитным материалом. Но особенность строения резинокордного слоя заключается в отсутствии периодичности по двум из трех направлений.

В работе рассматриваются два определения эффективных свойств композитного материала [3]. Они основаны на определении матриц эффективных податливостей  или жесткостей  материала. Из обратимости закона Гука следует, что матрицы  и   должны быть взаимнообратны.

Задачу поиска эффективных модулей Юнга для всего слоя можно свести к задаче на ячейке периодичности, применив условия симметрии. Попытки применить эти определения в данном случае приводят к противоречию. Представлены результаты решения подобной задачи в конечно-элементной программе.

В случае почти квадратной ячейки взаимнообратность обоих вариантов определения эффективных модулей соблюдается. Однако в случае вытянутой ячейки взаимнообратность матриц  и   нарушается. Рассмотренные определения эффективных свойств неприменимы для резинокордного слоя. Отсутствие периодичности существенно влияет на взаимнообратность матриц эффективных податливостей и жесткостей материала.

Предложено новое определение эффективных свойств резинокорда, учитывающее реальное строение шины и наличие слоев резины по краям исследуемого слоя. Применение нового определения значительно улучшило взаимообратность матриц  и  в рассматриваемой задаче.

Литература

1. Шешенин С.В., Демидович П.Н., Чистяков П.В., Муравлев А.В. Упругие свойства резинокорда. М.: Изд-во МГУ, 2009. 28 с.

2. Шешенин С.В., Ду Икунь. Модель резинокорда при умеренно больших деформациях // Сборник трудов 8-й Всероссийской научной конференции «Механика композиционных материалов и конструкций, сложных и гетерогенных сред». 2019. С. 101—108.

3. Победря Б.Е. Механика композиционных материалов. М.: Изд-во Моск. Ун-та. 1984. 336 c.

4. Шешенин С.В. Конспект лекций по методу конечных элементов.

Асимптотическое исследование пластин и стержней из материалов с искусственной структурой

Шешенин С.В.

Московский государственный университет имени М.В. Ломоносова, Москва

Материалы с искусственной структурой (метаматериалы), содержащие конечное число ячеек периодичности, обладают рядом оригинальных свойств. Среди них – отрицательный коэффициент Пуассона, связанность деформаций растяжения – сжатия и сдвига с изгибом и кручением. Примером могут быть пластины и стержни  из таких материалов. Отличительной чертой метаматериалов является периодичность структуры. В силу этого идеальным инструментом исследования служит асимптотический метод осреднения, который изначально был предложен для материалов, с периодически изменяющимися коэффициентами.

 Для пластин он разработан вплоть до третьего приближения для материалов имеющих периодическую структуру в плане пластины. Периодичности в поперечном направлении, вообще говоря, не требуется. Асимптотика строится по малому параметру, который есть стандартный для периодической пластины параметр, равный обратной величине числа ячеек периодичности в плане по одному направлению. Предполагается, что это тоже самое, что отношение толщины пластины к ее размеру в плане. В случае несимметричной структуры материала пластины асимптотический метод приводит к связанным определяющим соотношениям, в которых моменты и усилия связаны с деформациями и кривизнами. Важно, что жесткости на растяжение имеют первый порядок малости относительно малого параметра, жесткости связанности – второй порядок, а изгибные жесткости – третий.

Однако вполне возможно  допустить периодичность и в поперечном направлении. При этом возникают уже два малых параметра. Второй параметр – это единица, деленная на число периодических ячеек, укладывающихся по толщине. Если первый параметр мал, а второй нет, то имеет место быть описанная выше ситуация.  Если также мал второй параметр, то возникает другая ситуация и оказывается справедливым асимптотическое представление решения, типичное для среды, имеющей периодическую структуру по всем направлениям.

В докладе анализируется, что дает асимптотический метод в последнем случае. Показывается, что связь напряжений и деформаций также можно представить в неклассическом виде, в который входят собственно напряжения, моменты, деформации и вторые производные от перемещений. При этом жесткости материала также как и в двумерном случае имеют разные порядки относительно малого параметра. Этим дается ответ на фундаментальный вопрос: такой объект – это материал или конструкция? Асимптотическое исследование показывает, что при стремлении малого параметра к нулю моментные свойства исчезают. Поскольку строго материалом данные объекты могут называться при нулевом параметре, то следует считать их конструкциями относительно отмеченного выше свойства связанности в отличие от свойства отрицательности коэффициента Пуассона. Таким образом, показывается, что упругий материал с моментными свойствами нельзя получить в виде композита из компонентов, не обладающих моментными свойствами.

Работа выполнена при финансовой поддержке РФФИ (грант 19-51-53008).

Experimental study of polymers and structures for biomedical applications

Chentsov A.V.

Ishlinsky Institute for Problems in Mechanics RAS, Moscow

Modern chemical industry is much oriented to production of biodegradable polymers. Such materials gain many applications, particularly in medicine. Multitude of production technologies led to new polymers similar in content and at the same time different in mechanical properties. In evaluating the expected mechanical properties a number of mechanical tests are necessary, depending on the actual form of the final structure or intermediate billets. Note that due to specific applications of biodegradable polymers, the tests should be performed in a warm fluid. The most common polymer that we’ve considered was poly-L-lactide or PLA. A series of studies were performed on PLA microfibers (15-25 microns thickness). Even simple tensile testing required solution of a problem how to fix such small sample in the grips. For each batch we have determined the range of elastic modulus, average maximum load, average rupture deformation and yield limit. After passing the yield limit the PLA the samples showed a part of linear hardening with much lower average modulus. Special attention was paid to relaxation and creep of microfibers. Here, the adaptive exponential approximation was used with no more than two parameters of approximation.   A series of tensile tests was performed on plane films (180-220 microns thickness).  We have observed high plasticity in intact specimens. While exposure of the samples to active media (on a range of weeks) had changed the material behavior to be more brittle. The form of the fractured fragments (striped or layered) revealed the internal structure that was created, for example at layer-by-layer production of the films. Special needle equipped grips were designed for testing rings of PLA. The rings were cut from the tubes that were the billets for producing biodegradable stents (200 microns thickness). Tension of the rings might be not as accurate as tension of thin films, but it proved to be very useful for comparative tests of tubes materials. Using the femtosecond laser cutting we have produced several prototypes of biodegradable stents with auxetic design. The balloon-expansion of our stents (115% thickening) showed 25% elongation. This feature would increase trackability of these devices as shorter auxetic stents require less force to move along the blood vessel. Subsequent studies were devoted to different auxetic designs on plane samples. The concave hexagon (reentrant honeycomb) with straight sides is often an element of structure in auxetic constructions. We used the design of a concave hexagon in which a part of straight elements is replaced with "sinusoidal" elements. The sample was made by femtosecond laser cutting method out of a non-auxetic polyethyleneterephthalate (PET-a amorphous) planes. The transverse size of elements of hexagons was equal to sample thickness. The structures were subjected to monotonous uniaxial tension until the last moment when they still remained plane. As a result of the experimental data analysis, comparison of mechanical properties was given for faultless sample and constructions in which one horizontal or vertical element in the central area of a sample was removed. We conclude that lack of one horizontal element of construction, has little influence on auxetic properties of these constructions unlike the structure with one vertical element being absent. Calculations of similar structures using FEM for linear elastic or elastic-plastic material were performed.  The elastic energy functional was also implemented in a discrete-continuum numerical model. The parameters of these models were fitted for best correspondence with experimental results.

Mesoscopic design and characterization of Auxetic Materials

Lingling Hu, Minghui Fu

School of Engineering, Sun Yat-sen University, Guangzhou

The nonlinear in-plane shear modulus of re-entrant hexagonal honeycombs under large deformation is analytically derived by studying the mechanical behaviors of cell structures, which is then verified by numerical simulations. A nonlinear modified factor is brought forward to characterize the difference of the honeycomb’s shear modulus under the large and the small deformation, revealing its independence from the honeycomb’s relative density. The effects of both strain and cell geometry on the honeycomb’s shear modulus are investigated. The shear modulus of the re-entrant honeycombs is compared with that of the conventional honeycombs. Different from the predictions by the classical continuum theory, the present study shows that the shear modulus of the re-entrant honeycomb with negative Poisson’s ratio is not always higher than that of the conventional honeycomb with positive Poisson’s ratio, which is dominated by the geometry of cell structures.

It is generally acknowledged that the indentation resistance or hardness of auxetic materials is higher than that of their conventional counterparts under elastic deformation. However, this property of the auxetic material may not always be superior to that of the non-auxetic materials when the deformation is relatively large with plasticity considered. In this study, we come up with an index to quantitatively depict the indentation resistance of the hexagonal honeycombs under large deformation. The indentation resistance of both the auxetic and nonauxetic hexagonal honeycombs is compared and discussed. Results show that in the premise of honeycombs possessing the same relative density, the indentation resistance of auxetic hexagonal honeycombs is not always higher than that of the non-auxetic honeycombs. This phenomenon is verified by the numerical simulations. Further analysis shows that there is a critical value of the absolute value of Poisson’s ratio, which is determined by the cell-wall length ratio, to estimate the higher indentation resistance between the auxetic and non-auxetic hexagonal honeycombs. The influence of indentation velocity is also analyzed based on numerical simulations.

Designing lightweight composites and structures for negative thermal expansion

Minghui Fu, Lingling Hu

School of Engineering, Sun Yat-sen University, Guangzhou

The regulation of thermal expansion plays an important role in the engineering. A new type of metamaterial with NTE effect is designed by means of reinforcing the reentrant honeycomb. The analytical formulas of CTE, equivalent Young’s modulus and Poisson’s ratio of this material has been deduced by adopting Timoshenko beam theory, and their validity has been verified by numerical simulation. The analytical formulas are applicable for the case that the thickness of reinforcement panel is small. When the thickness is large, the modified results are also given. Using the analytical formulas, the material can be quantitatively designed according to the practical requirements.

CTE of the material can be achieved to regulate and control from negative to positive by changing the geometric parameters, and the negative Poisson’s ratio effect of the reentrant honeycomb can be preserved simultaneously. The approaches to achieve the maximum NTE and zero thermal expansion are discussed when the inclination of the inclined panel in the honeycomb is changed. By choosing the appropriate geometric parameters, CTE of NTE of this material can be several times of that of conventional material and zero thermal expansion in both two directions can be achieved, which has special practical value in the engineering. Furthermore, the design idea of the material proposed in this paper is also generalized to 3D materials and the analytical formulas of CTE is also given. Since the formulas of CTE of 3D material is similar to that of 2D material, the regulative method of CTE of 2D material is also applicable for the 3D material. Although the substrate materials used in this paper are limited to common industrial materials, in fact, the realization mechanism of NTE and zero thermal expansion can also be extended to extreme materials in case that CTEs of the two kinds of substrate materials are quite different.

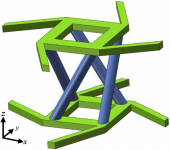
Mechanical metamaterial with tension-torsion coupling effect

Minghui Fu, Lingling Hu, Zuoqiu Liu   

School of Engineering, Sun Yat-sen University, Guangzhou

A new type of metamaterial is designed by adding inclined rods between tetra-chiral planes. When the metamaterial is subjected to the load perpendicular to the chiral honeycomb plates, the deformation of the inclined rods will drive the rotation of the chiral planes, and then produce the tension-torsion coupling effect. Both the experiments and numerical simulations show that the metamaterial has significant tension-torsion coupling (TTC) effect. With the increase of the cells number, the TTC effect of the proposed metamaterial at different strains first increases, then reaches the peak value, finally decreases. Take the TTC effect of metamaterial at the strain of 1% as an example, the torsion angle of metamaterial reaches its peak value of 11.36∘ at n = 8, and remains 4.44∘ at n = 25, which is big advantage compared to other 3D TTC metamaterial in literatures. The size effect of metamaterial is studied, and result shows that the size effect of the proposed metamaterial in the z direction can be neglected when the cells number of metamaterial along z direction is more than 5. The stress and deformation of struts within the metamaterial are studied. Both inclined rods and the square loops mainly bear tensile deformation while the main deformation of ligaments is out-of-plane bending deformation. The compression deformation of innermost inclined rods is the biggest, decreasing outward, and then gradually turns into tension deformation. Thus, when the compression strain increases, the innermost inclined rods enter the instability state first. As the compression strain increases further, the instability zone gradually expands outwards, and the torsion angle of the metamaterial increases slowly then enter the platform stage. The design concept provides a framework to develop tension-torsion coupling metamaterials. For example, replace the tetra-chiral honeycomb by tri-chiral honeycomb or hexa-chiral honeycomb, other TTC metamaterials are developed.